コレクション python 标准差公式 650002

在
数据标准化与Python实现 数据标准化(Normalization):将数据按照一定比例进行缩放,使其落入到一个特定的小区间。 MinMax标准化,指对原始数据进行线性变换,将值映射到 0,1之间。 式中,x为原始数据的数据,xmin为原始数据的最小值,xmax为原始数据的最大 在数学上,标准偏差等于方差的平方根。 本教程将演示如何在 Python 中计算列表的标准偏差。 使用 statistics 模块的 pstdev() 函数在 Python 中计算列表的标准偏差 pstdev() 函数是 Python 的 statistics 模块下的命令之一。statistics 模块提供了对 Python 中的数值数据执行统计
Python 标准差公式
Python 标准差公式-Python 风格规范(Google) 本项目并非 Google 官方项目, 而是由国内程序员凭热情创建和维护。 如果你关注的是 Google 官方英文版, 请移步 Google Style Guide 以下代码中 Yes 表示推荐,No 表示不推荐。 分号 不要在行尾加分号, 也不要用分号将两条命令放在同一行。 行长度 每行不超过80个字符 以下情况除为什么使用Excel计算标准差与手动计算的值不一样? 手算: 相对标准偏差的计算公式 90;
Python 使用pandas和numpy计算标准差的区别 简书
std()函数就是初高中学的标准差numpystd() 求标准差的时候默认是除以 n 的,即是有偏的,npstd无偏样本标准差方式为加入参数 ddof = 1;(推荐学习:Python视频教程)pandasstd() 默认是除以n1 的,即是无偏的,如果想和numpystd() 一样有偏,需要加上参数ddof=0 ,即pandasstd(ddof=0) ;在统计学中,多年的经验总结出: 直接上代码 #调出numpy import numpy as np arr = 2, 4, 6, 8, 10, 12 # 要计算的数值 # 求均值 arr_mean = npmean(arr) # 求方差 arr_var = npvar(arr) # 求标准差 arr_std = npstd(arr, ddof=1) # 数值输出 print("平均值为:%f" % arr_mean) print("方差为:%f" % arr_var) print("标准差标准差(Standard Deviation,又常称均方差)是一个数字,描述值的离散程度。 低标准偏差表示大多数数字接近均值(平均值)。 高标准偏差表示这些值分布在更宽的范围内。 例如:这次我们已经登记了 7 辆车的速度: speed = 86,87,,86,87,85,86 标准差是: 09
公式: Python实现: 这里直接调用skimage方法,当然还有其他(不排除其他方法更好的可能),就我知道的ENVI就可以计算glcm相关的,Python调用google earth engine包也不是不可以。 等等方法很多 计算灰度共生矩阵; # 计算距离为1,2和角度为0度,90度的GLCM的ASM def 自定义标准差标准化函数 def StandardScaler (data) data= (datadatamean ())/datastd () return data ##对菜品订单表售价和销量做标准化 data4=StandardScaler (detail 'counts') data5=StandardScaler (detail 'amounts') data6=pdconcat ( data4,data5,axis=1) print ('标准差标准化之前销量和售价数据为:\n', 当 Python 一维数组是输入时,Numpystd() 函数计算数组中所有值的标准差。 import numpy as np arr = 10, , 30 print("1D array ", arr) print("Standard Deviation of arr is
Python 标准差公式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 |
 方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 | 方差和标准差variance Standard Deviation 数据分析教程 盖若 |
 方差和标准差variance Standard Deviation 数据分析教程 盖若 | 方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 |
 方差和标准差variance Standard Deviation 数据分析教程 盖若 | 方差和标准差variance Standard Deviation 数据分析教程 盖若 | 方差和标准差variance Standard Deviation 数据分析教程 盖若 |
方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 |
方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 |
方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 | 方差和标准差variance Standard Deviation 数据分析教程 盖若 |
 方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 | 方差和标准差variance Standard Deviation 数据分析教程 盖若 |
 方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 | 方差和标准差variance Standard Deviation 数据分析教程 盖若 |
 方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 | 方差和标准差variance Standard Deviation 数据分析教程 盖若 |
 方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 |
 方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 | 方差和标准差variance Standard Deviation 数据分析教程 盖若 |
 方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 | 方差和标准差variance Standard Deviation 数据分析教程 盖若 |
 方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 |
 方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 |
 方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 |
方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 | 方差和标准差variance Standard Deviation 数据分析教程 盖若 |
 方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 | 方差和标准差variance Standard Deviation 数据分析教程 盖若 |
 方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 |
 方差和标准差variance Standard Deviation 数据分析教程 盖若 | 方差和标准差variance Standard Deviation 数据分析教程 盖若 | 方差和标准差variance Standard Deviation 数据分析教程 盖若 |
 方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 |
 方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 | 方差和标准差variance Standard Deviation 数据分析教程 盖若 |
 方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 | 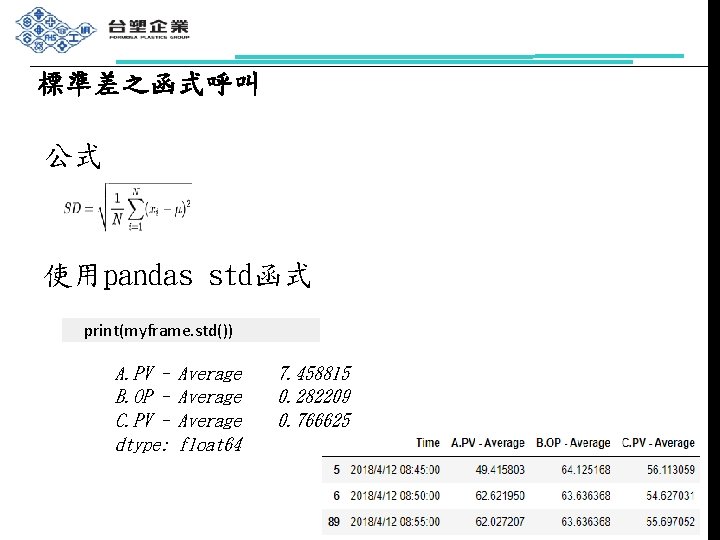 方差和标准差variance Standard Deviation 数据分析教程 盖若 |
 方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 |
 方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 |
 方差和标准差variance Standard Deviation 数据分析教程 盖若 | 方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 |
 方差和标准差variance Standard Deviation 数据分析教程 盖若 | 方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 |
方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 | 方差和标准差variance Standard Deviation 数据分析教程 盖若 |
 方差和标准差variance Standard Deviation 数据分析教程 盖若 | 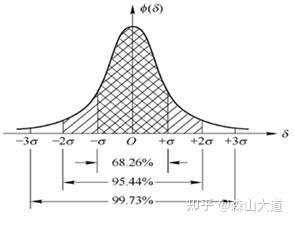 方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 |
方差和标准差variance Standard Deviation 数据分析教程 盖若 | 方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 |
 方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 | 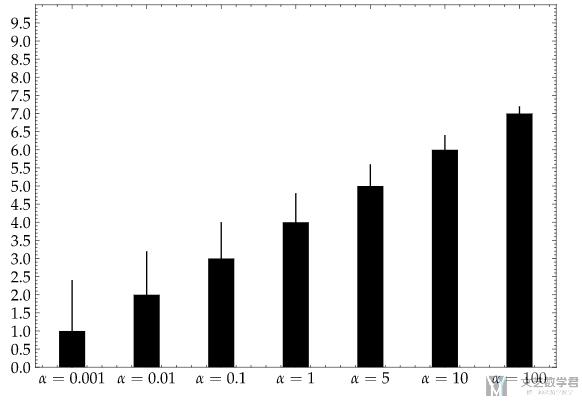 方差和标准差variance Standard Deviation 数据分析教程 盖若 |
 方差和标准差variance Standard Deviation 数据分析教程 盖若 | 方差和标准差variance Standard Deviation 数据分析教程 盖若 | 方差和标准差variance Standard Deviation 数据分析教程 盖若 |
 方差和标准差variance Standard Deviation 数据分析教程 盖若 | 方差和标准差variance Standard Deviation 数据分析教程 盖若 | 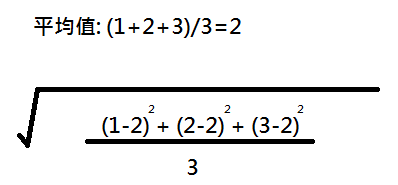 方差和标准差variance Standard Deviation 数据分析教程 盖若 |
 方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 |
 方差和标准差variance Standard Deviation 数据分析教程 盖若 |  方差和标准差variance Standard Deviation 数据分析教程 盖若 |
numpystd() 求标准差的时候默认是除以 n 的,即是有偏的,npstd无偏样本标准差方式为加入参数 ddof = 1; pandasstd() 默认是除以n1 的,即是无偏的,如果想和numpystd() 一样有偏,需要加上参数ddof=0 ,即pandasstd(ddof=0) ;DataFrame的describe()中就包含有std(); demo: >>> a array(0, 1, 2, 3, 4, 5, 6, 7, 8, 9) >>> npstd(a, ddof = 1) >>>用Python求均值与方差,可以自己写,也可以借助于numpy,不过到底哪个快一点呢? 我做了个实验,首先生成9百万个样本: nlist=range(0,) nlist=float(i)/ for i in nlist N=len(nlist) 第二行是为了让样本小一点,否则从1加到9百万会溢出的。
コメント
コメントを投稿